Combining factors in a portfolio

About a month ago, I wrote about the decline in the performance of factor portfolios. I closed with a hopeful note that a combination of different factors can still be used to improve portfolio performance. 

Given the alarming number of factors identified in the academic literature, most of which stop working the day after they have been published, a lot of academics have started to explore what the minimum number of factors is that we need to use to exploit the benefits of factor investing. However, as Victor deMiguel and his colleagues have pointed out, the problem with these efforts so far has been that they ignored transaction costs. That doesn’t really help practitioners like me because transaction costs are real and have to be taken into account if you are running a portfolio. But now we have at least a first answer to this problem in the form of the research of Victor deMiguel linked to above.

These guys took a total of 51 factors described in the literature (which includes every factor you have ever heard of and excludes factors that are so exotic that nobody ever uses them anyway) and then tried to identify which factors provide the best combination in a portfolio. 

In order to understand which factors are expected to do well when combined in a portfolio, one has to understand one thing about portfolio construction that often gets ignored: In order for an asset (or in this case a factor) to get a large weight in a portfolio returns don’t matter and volatility doesn’t matter. What matters is the ratio of returns/volatility. In other words, assets with higher risk-adjusted returns get a larger weight in a portfolio not assets with a higher return or lower volatility. In my experience, too many investors don’t know that and are then surprised when a portfolio optimiser tells them to use some assets that have seemingly lower returns or higher volatility than what they expect by looking at each asset class individually. 

As an aside, I can also always tell if a company uses properly calculated optimised portfolios or has just created a portfolio that intuitively looks diversified and seems to make sense. You wouldn’t believe how many companies don’t really optimise their portfolios simply because it is easier to sell a portfolio that looks nice than one that works.

In any case, deMiguel and his colleagues find that in the absence of transaction costs they only need to combine six different factors to capture the full benefit of factor investing and maximise the Sharpe ratio of the resulting portfolio: Quarterly earnings surprises, return volatility, asset growth, 1-month price momentum, profitability and market beta. 

Note that neither value nor size or the classical 12-month price momentum are used to build this optimal multi-factor portfolio. The reason for that is that while all of these factors have pretty high returns on their own, their volatility is also pretty high and hence their risk-adjusted returns are lower than for the other factors and thus they are excluded from the optimal portfolio. 

The problem in practice is, though, that replicating any factor involves transaction costs because the factor portfolio composition changes as some stocks drop out of the factor portfolio while others are newly included. 

A portfolio with more factors in it has a distinct advantage in a world where investors have to pay transaction costs. A stock may drop out of one factor portfolio but may be introduced into another factor portfolio at the same time. Hence, the portfolio manager can net out these two trades and avoid transaction costs on these altogether. The more factors a portfolio contains, the more likely it is that such netting is possible. But the more factors a portfolio contains, the more expensive transactions will become because the trades become smaller and smaller since each factor has a lower allocation in the overall portfolio. 

DeMiguel and his colleagues find that for a US Dollar investor the optimal factor portfolio combines a total of 15 factors, the six mentioned above as well as nine more that you can look up yourself in their paper if you are interested. Importantly, in the presence of transaction costs the traditional factors like value or momentum suddenly enter the portfolio again because they have high enough risk-adjusted returns and low correlation to the original six factors so that it becomes more likely that they will absorb stocks that would otherwise have to be sold out of the portfolio or provide stocks to the portfolio that would otherwise have to be bought in the market.

But before you rush out and duplicate these multi-factor portfolios be aware that the exact number of factors and the exact factors to combine in an optimal portfolio depends on your transaction costs, your home currency, and your investment universe. So do your own work and don’t just copy-paste. It’s called optimisation for a reason.

Contribution to transaction costs if a factor is traded in isolation and in the optimal multi-factor portfolio

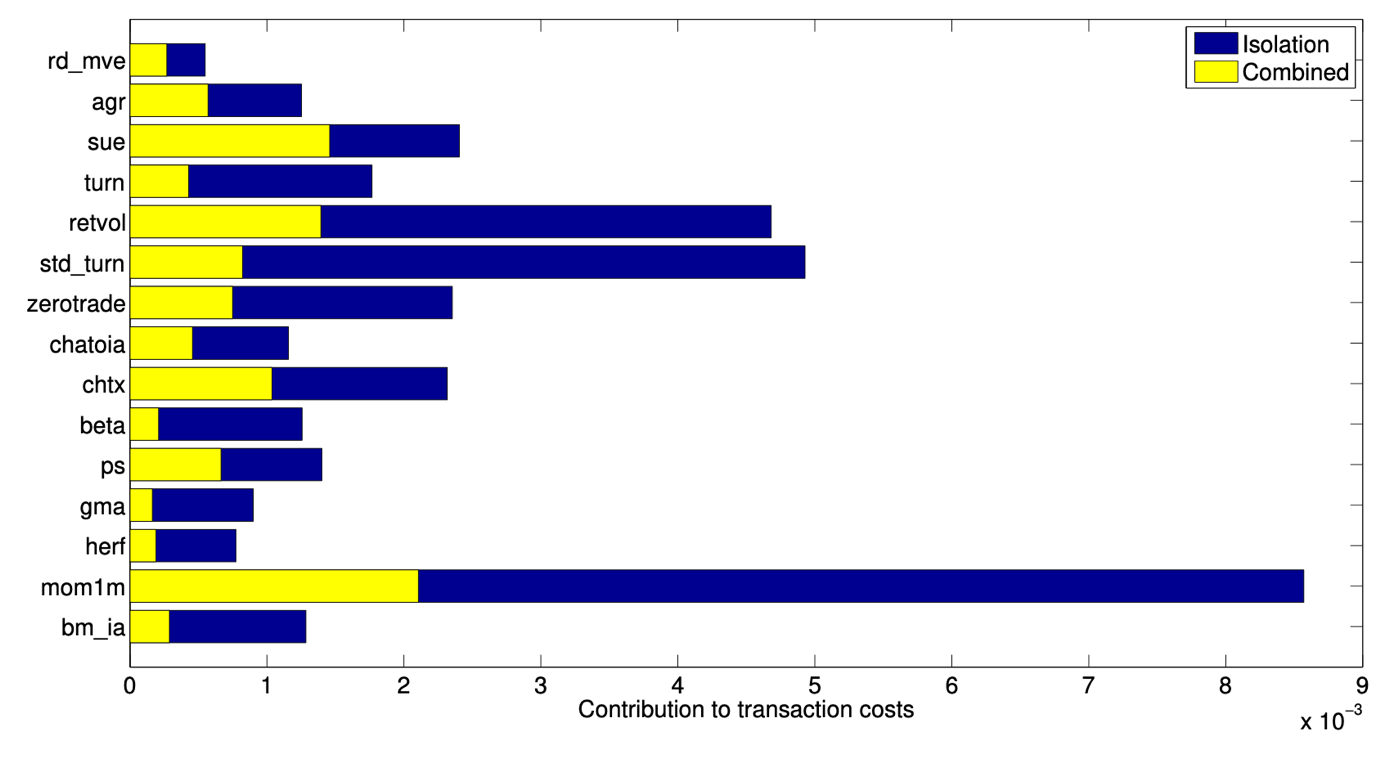
Source: deMiguel et al. (2017).