Some time ago, I wrote a post about equal-weighted portfolios and why they work in terms of factor exposure. I also featured in a podcast on David Stevenson’s excellent blog, The Adventurous Investor. If you haven’t subscribed, yet, do so now. You will not regret it.
But there is more to the story, as you may have guessed. To me, the key benefit of equal-weighted portfolios is that they provide a robustly good outcome, even if you are wrong.
A couple of guys from Vanguard and Ohio State University recently looked at factor portfolios and asked whether they can be combined via equal weighting into a multi-factor portfolio that beats the market.
They compared a multi-factor portfolio of three equal-weighted factor portfolios (value, momentum and quality) with the market as well as ‘optimised portfolios’ using mean-variance optimisation without constraints (the three individual factor portfolios could have any weight between 0% and 100%) and constrained mean-variance portfolios where the individual factor portfolios were pushed toward a more equal weight by restricting their weight between 10% and 40%. They also compared the equal-weighted multi-factor portfolio with an unconstrained minimum variance portfolio and a constrained minimum variance portfolio.
I’ll spare you the details, because like in every other study on the subject, the result was that on average, the equal-weighted portfolio outperforms the mean-variance optimized portfolio and the minimum variance portfolio.
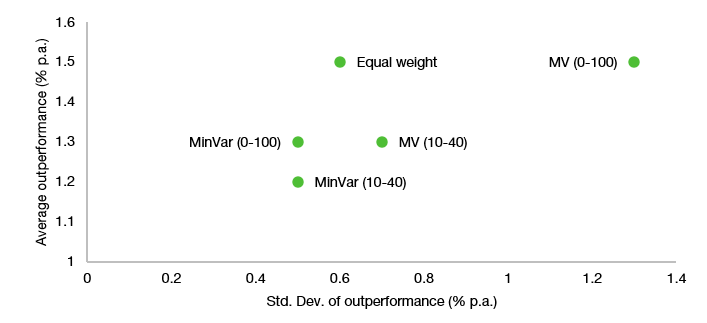
However, what was interesting about their study is that they also showed how much the average outperformance of the different multi-factor portfolios varied depending on the actual path markets took. The chart below shows the average annual outperformance vs. the market on the vertical axis and the variation of this outperformance. As you can see, the equal-weighted portfolio has a similar outperformance on average as the unconstrained mean-variance portfolio, but the variation around the average return is much higher for the mean-variance portfolio. In other words, you are just as well off with the mean variance portfolio as with the equal-weighted on average, but if the market doesn’t behave as you expect, you can be way off with your mean-variance optimised portfolio while the equal-weighted portfolio will do just fine. Not great, but fine.
Average outperformance of portfolio and the variation of that outperformance
Source: Khang et al. (2023)
Note also, that for the minimum variance portfolios, the variation around the average outperformance is even lower than for the equal-weighted portfolio, though the size of the outperformance is significantly smaller. But when it comes to the stability of returns, minimum variance portfolios are unbeatable. Which shouldn’t surprise you because that is how they were constructed in the first place. The clue is in the name.
But here is another chart for you. This time, I look at the information ratio, i.e. the average outperformance divided by the average variation of that outperformance over time (tracking error) and how much that information ratio varies depending on market behaviour. You can see that compared to the mean-variance portfolios, the information ratio of the equal-weighted portfolio is much higher, simply because the outperformance is so much more reliable. Minimum variance portfolios can compete with equal-weighted portfolios in that respect because their variation of outperformance is so small, but the price an investor has to pay is lower outperformance, i.e. lower returns. If you ask me, I love both minimum variance portfolios and equal-weighted portfolios. What I don’t like are optimised portfolios because, well, they are simply not optimal.
Information ratio of portfolios
Source: Khang et al. (2023)





Thanks for the post!
Does the average outperformance account for the costs of monthly rebalancing here?
Where would the capitalization weighted portfolio stand in there?