Should we abandon fair value calculations? Part 1

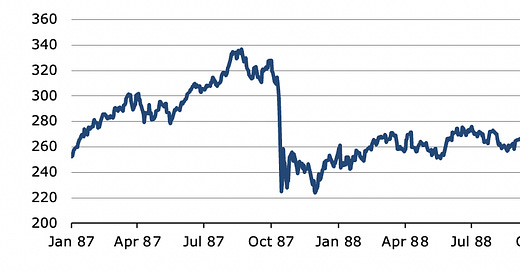
Some time ago, a reader sent me a collection of essays by a strategist from a renowned asset manager. In one of these essays, the author tried to tackle a seemingly philosophical problem and observed that the price chart of stocks or a market index like the S&P 500 is not time invariant, i.e. one cannot reverse the chart in time and expect to see something like a real chart. The classic example is a market crash like the one in October 1987. The S&P500 that day dropped more than 20% in one day and then slowly recovered. If one would look at the chart in reverse, it would be a situation where the S&P500 slowly declines and then suddenly jumps more than 20% in one day. That doesn’t happen in real life.

The S&P 500 around the 1987 crash

Source: Bloomberg

Then, the author argues that this arrow of time in stock markets is like the famous arrow of time introduced by the Second Law of Thermodynamics in physics. The Second Law of Thermodynamics basically states that the entropy in a closed system increases and the system will over time drift towards the equilibrium state of maximum entropy.

The classic example is a drop of ink in a water jar. The ink will slowly dissolve in the water until the whole jar is a pale blue colour, but it doesn’t happen that a jar full of dissolved ink suddenly separates into water and a drop of ink. Therefore, the author argues, that it is this arrow of time that leads stock markets to drift towards the equilibrium given by the fair value of the market or the stock.

With all due respect but let me call bs on that.

This is an analogy that only someone who didn’t study thermodynamics can make. In fact, if you understand the analogy correctly, it might lead one not to the conclusion that markets have to drift towards fair value, but exactly the opposite, namely that it is incredibly unlikely that markets will ever be close to fair value. This obviously puts into question one of the most basic tenets of all investing, namely that we can estimate the fair value of an asset or market and that this fair value is a reasonable anchor for predicted market moves.

What the Second Law really says

As someone who studied physics and maths at university, I had my fair share of thermodynamics lectures and while there are many ways to formulate the Second Law (e.g. the formulation given by Carnot or the one by Kelvin), I think it is fair to say that since the formulation of quantum mechanics, the most universally accepted definition is the one given by Boltzmann. To make a long story short, the Second Law states that the entropy S of a closed system has to stay constant or must increase over time, where S is given by:

S = k•ln(W)

In that equation, k is the Boltzmann constant 1.38•10-23 J/K and ln(W) is the probability that the system is in a given state. To use the analogy of the drop of ink in the water jar, there are far more states that correspond to the individual ink molecules spread out all over the jar than there are states that correspond to the ink molecules all closely next to each other. So, the system will drift towards the most likely outcome which is one where the ink molecules are spread out more or less evenly across the jar. That is not to say that it could theoretically happen that the ink drop remains separated, it just is extremely unlikely.

You can think about it this way. If you play lotto, every combination of numbers is equally likely but there are far more instances where 6 numbers are spread out all over the total field of 48 or 50 numbers to choose from than instances when the six winning numbers form one sequence of ascending numbers (e.g. 1, 2, 3, 4, 5, and 6).

From the Second Law to investing

And this is where the Second Law becomes interesting for investors. If you think about it, the valuation of a stock is given by all the different future cash flows discounted to the present day. Similarly, though much easier to deal with for our purposes, the fair value of the S&P 500 is simply the weighted average of the fair value of all stocks in the index. Each individual stock in the S&P 500 may deviate from its fair value, but the index overall may still end up at fair value if these deviations cancel each other out.

But what is more likely to happen? That all the individual valuations of each stock in the S&P 500 line up in such a way that the result is an S&P 500 at fair value? Or that the individual valuations line up in such a way that you get any number other than the fair value?

That the S&P 500 should be at fair value is about as likely as playing a game of lotto, where you have to select 500 numbers out of one million and ending up with a winning combination that is the numbers 1 to 500 in a row.

I think this makes it clear that it is almost impossible for the S&P 500 to be at or anywhere near fair value. Similarly, you can do the same mental exercise with the future cash flows of a stock and ask yourself, how likely it is that the future cash flows will line up in such a way that the fair value of a stock is identical or even anywhere close to the current share price.

And if the S&P 500 or any stock practically never is at or near fair value, the question is why bother calculating the fair value in the first place? If the Second Law applies and a market drifts towards the most likely state, it will never end up at fair value. If true, that would mean that fair value calculations are entirely useless.

Unless, of course, there is some magic force that pulls the S&P 500 or an individual stock towards fair value over time. This is a question where thermodynamics may also give us some answers. But you will have to wait until tomorrow to read about that.