Should we abandon fair value calculations? Part 3
Over the last two days, I have done my best to lose as many readers as possible by talking about the Second Law of Thermodynamics, its implications for finance, and the ergodicity problem. For the few readers whose eyes haven’t glazed over yet, I want to talk about an intriguing experiment today and what that means for financial markets.
The bad news for the philosophically minded readers is that this is the last part in this short series of articles. The good news for all other readers is that this is the last part in this short series of articles. Lighter fare will be served tomorrow again.
When discussing the ergodicity problem in economics yesterday, I mentioned that the traditional assumption underlying expected utility economics may be violated in real life. In particular, the average of random deviations from fair value may not go towards zero and the share price may in fact not gravitate towards whatever the fair value of the share is. But financial markets are reflexive and if investors behave as if expected utility economics is true and random fluctuations even out over time, then they may make that a reality with their trading.
This is where a group of researchers from Denmark come into play. They have set the first experiment to test if investors behave differently than what expected utility economics predicts. People were asked to play a lottery. They were given DKK1,000 (c. $155) and asked to use this money to make investments in risky assets. The participants were asked to come in on two days where they were confronted with different investments.
On one day, they were presented with an additive gamble. It was essentially the flip of a coin, where one outcome created a gain of DKK300 and the other a loss of DKK200. The more often the participants played that game the more likely it would be that they ended up with the expected profit of $5. The amount the participants could win or lose in each gamble varied so that risks changed and the researchers could examine the risk preferences of the participants.
On the other day, the participants were presented with a multiplicative gamble. If the coin flip ended up heads, the participants would make a profit of 30%, if it came up tails, they would lose 20% of their money. Again, the returns for gains and losses changed so that researchers could examine the different responses for different risk levels. In order to assure that participants understood the game, they were participating in a one-hour training session before each day’s experiment began.
If expected utility economics is right, participants would behave the same way in both setups because expected utility theory assumes people maximise returns and the experiment is calibrated in such a way that in both conditions expected return and expected volatility are the same. But if participants changed their behaviour it would indicate that ergodicity economics is right and people understand that the path matters and they try to optimise ending wealth instead of returns.
And guess what, when confronted with the multiplicative environment, the participants changed their behaviour and became much more risk averse. Participants understood that in the face of 30% gains vs. 20% losses, their losses could increase dramatically over time and so they were much more reluctant to bet large amounts or refrained from participating in particularly risky gambles with potentially large losses.
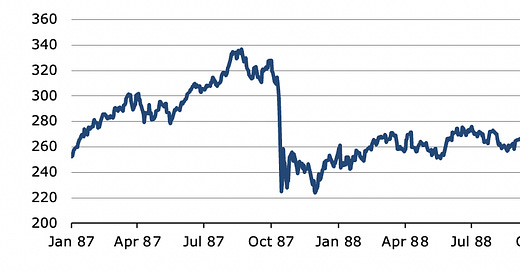
This result provides an entire series of important insights that need to be investigated further. First, even though people have vastly different risk aversion, this risk aversion is not just determined by an individual’s psychology. It is also determined by the circumstances, she is put in. Second, it provides a possible explanation why people are more risk averse than expected utility economics predicts. In real life, most investors hold far less risky portfolios than would be optimal given their investment horizon, and the expected return and risk of a portfolio. And as every wealth manager knows, it is incredibly hard to get people to increase their equity allocation in a portfolio above their comfort level even if that higher equity allocation would be beneficial to their wealth and financial security. Third, this result may help explain the equity premium puzzle. The equity premium puzzle is the observation that in real life the excess return of equities above bonds is much higher than expected utility economics predicts. And fourth, it may explain why markets famously go ‘up the stairs, down the escalator’. Remember the chart of the S&P 500 during the October 1987 crash that started this entire series? Back then I said that this chart shows there is an arrow of time in markets. Markets don’t suddenly jump 20% higher in one day, but they can easily drop 10% or more in a day as we again found out last year. Ergodicity economics provides a simple answer to this observation. Because people try to maximise ending wealth and not returns, they are simply refusing to enter gambles where they can lose a large amount of their wealth even if the expected return improves. And because many investors independent of their risk aversion refuse to participate in stock markets at the same time, the drop can be fast and furious.
The S&P 500 around the 1987 crash
Source: Bloomberg
Note also, that the experiment doesn’t rely on behavioural factors and thus is not based on the assumption of ‘irrational’ behaviour. People are behaving perfectly rational in the experiment if we use ergodicity economics as a model. As I said, it is early days for ergodicity economics, but it could well be that people are much smarter than expected utility economics predicts and at the same time more rational than behavioural economics thinks.