The world’s most common forecasting mistake

Forecasting is hard (especially about the future, one might add), but it is made harder when people use inadequate forecasting techniques. If you want to know how to make forecasts, I think there is no better place to start than to read Philip Tetlock’s Superforecasting: The Art and Science of Prediction. Obviously, I don’t have the space here to fully discuss this book, but I want to focus on one forecasting error that irks me time and again: linear extrapolation.

In my view, extrapolating recent trends into the future is the most common mistake forecasters make in any field. In sports, pundits extrapolate the last three to five matches of a team to talk them into title contenders. In politics, I hear cries of ‘socialism’ every time a government increases regulation in some area or tries to change rules about the environment. And in business and finance, there are so many forecasts that predict that some technology or trend will grow into a trillion-dollar business in the next decade, etc.

But a winning streak doesn’t mean a team will win a championship. Government regulation in one area does not lead to a slide into socialism and AI isn’t going to be a $15.7 trillion industry by 2030, as this report claims.

Typically, the mistake starts by using recent growth rates, then adapting them a little bit to reflect the opinion of the pundit about the future (if the pundit expects growth to slow down, the growth rate is adjusted downward, for example) and then extrapolating that growth rate many years into the future. The result is a projection that looks like the chart below.

How people forecast growth

Source: Liberum

Normally, pundits are careful not to show the chart as I did because it clearly shows the ridiculousness of the forecast. It predicts literally that trees grow into the sky. Instead, pundits often just truncate the forecast period so as to make the forecast look reasonable. Something like this:

A typical pundit forecast

Source: Liberum

I recently came across a nice cartoon illustration of the mistake made here:

The problem with extrapolating recent trends

Source: Jessie Robinson

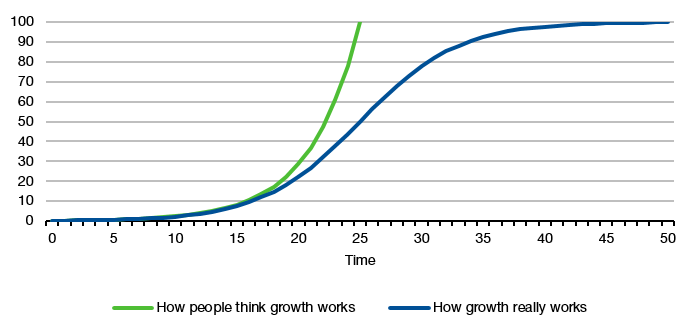
But of course, trees don’t grow into the sky and dogs don’t look like prehistoric monsters. For every trend there is a countertrend and resources are limited. Both countertrends and a lack of resources limit how long a trend can continue. In effect, growth in the real world is always, ALWAYS constrained and should be modelled using the logistic function instead of a simple exponential growth function.

How growth really works

Source: Liberum

Again, the chart above makes it look obvious, but as I said above, pundits don’t use these kinds of charts. Instead, they reduce the time frame they show to make their forecasts look more reasonable. Well, if we do that with the last chart, you can see how poor the forecasts of pundits are even on shorter time horizons.

The error inherent in pundit forecasts

Source: Liberum

This is why I react so allergic to pundits. It’s not just that these forecasts are based on a lack of mathematical understanding and (quite frankly) basic maths training. It is that they are incredibly misleading and lead decision-makers to make harmful decisions. Business leaders who believe that AI will be a $15 trillion business in the next decade are inclined to invest heavily in this technology, thus draining resources from other technologies that may be more promising, cheaper or simply better suited for the job at hand (just think of all the businesses that invested in blockchain technology even though it wasn’t fit for the purpose it was used for). Meanwhile, sports teams may decide to buy players for large fees because they had one good season. And investors may decide to buy stocks of companies that have gone up in the last couple of years.

Always remember, trees don’t grow into the sky and all growth comes to an end. The trick to a good forecast is to know where the limit to growth is and how close we are to this limit not how fast growth is going to be in the next couple of years.