Why why why was this article written?

The latest edition of the Financial Analysts Journal (FAJ) has an article called “In Defence of Portfolio Optimization”. In it, the authors challenge the notion that traditional mean-variance optimization is inferior to simpler approaches like the equal-weighted portfolio. Most notably, Victor DeMiguel and his colleagues showed about a decade ago that a simple equal-weighted asset allocation approach performs better in real life than a portfolio optimized with Harry Markowitz’s mean-variance optimization approach. The reason why this is the case is because we are largely unable to forecast returns and mean-variance optimization reacts very sensitively to those forecasts. Hence, if you get the return forecast wrong, your asset allocation is likely to perform poorly if you have used mean-variance optimization. As I have described in some detail here, the equal-weighted asset allocation approach takes this uncertainty about the future to its radical conclusion and assumes we know nothing about the future. And in practice, this seems to be often the better assumption to make.

Of course, the followers of modern portfolio theory could not let that result stand and launched an initial challenge by Mark Kritzman and his colleagues that tried to show that if you use “sensible” return forecasts you would do better than with an equal-weighted portfolio. This challenge was so clumsily designed that it was rightfully ignored since nobody will ever be able to agree what constitutes a “sensible” return forecast. In fact, the entire article looked to me more like an exercise in reverse-engineering where return forecasts were “massaged” long enough to create a mean-variance optimized portfolio that outperforms an equal-weighted portfolio.

But now, the big guns have been brought out by the new article. In it, the authors show that even if you have no forecasting ability, the “expected utility” of an investor will be higher if she uses a mean-variance optimized portfolio. The authors furthermore run simulations of market returns and showed that mean-variance optimization is superior (in terms of Sharpe ratio) to equal-weighted portfolios as long as there is a moderate amount of forecasting ability. Finally, the authors showed in empirical evaluations between 2000 and 2014 that mean-variance optimized portfolio outperform equal-weighted portfolios for most standard forecasting models.

These are serious efforts to save another pillar of modern portfolio theory from being destroyed. Unfortunately, in my view, some of the assumptions made in the FAJ article are not realistic in practice. First and foremost, the authors of the article work with a utility function in their theoretical model as well as in their simulation and empirical experiments. While this may be academically sound, the problem I have with utility functions is that the results are sensitive to the risk aversion parameter l, which – unfortunately – is unknown in real life. What makes things worse is that the risk aversion parameter l cannot be measured accurately in practice. Within a behavioural finance framework one can even show that “expected utility theory is an utterly implausible explanation for appreciable risk aversion over modest stakes: Within expected-utility theory, for any concave utility function, even very little risk aversion over modest stakes implies an absurd degree of risk aversion over large stakes”. In other words, by relying on an expected-utility framework in their article, the authors have used a framework that has no validity in real life to show that mean-variance optimization is superior in real life…

Even so, there are other assumptions the authors make that are hard to match in practice. In their simulation approach, they show that investors with a moderate amount of forecasting ability can lead to outperformance of the mean-variance optimization technique. The problem is that there is no empirical evidence that shows that professional forecasters are better than a random walk as I have explained here and here. So, assuming that an investor has moderate forecasting ability is one thing. Providing evidence that this is possible in practice is another thing altogether.

Which brings me to the authors’ historical tests. In these tests they build on the work of Welch and Goyal who have tested the out-of-sample forecasting performance of different forecasting models. In the FAJ article the authors then use ten years of historical data to estimate returns of different assets for the next month and calculate the mean-variance optimized portfolio. After a month, the same procedure was be repeated with a new one-month forecast and so on. Unfortunately, that is not how portfolio optimization works in practice. I know of no asset allocator who calculates the optimal portfolio on a monthly basis. Typically, portfolio optimization is done only on much longer time scales of one year or more. Not even portfolio rebalancing is typically done on a monthly basis, let alone a full-scale optimization. And this is where the problem starts. As the paper of Welch and Goyal shows, forecast errors of the different models that are used in the FAJ article increase rapidly as the investment horizon increases. The relative forecast error is very small for investment horizons of one month or one quarter but grows exponentially as one approach investment horizons of one year or more. And this means that the results of the FAJ article likely overstate the performance of the mean-variance portfolios.

For these reasons, I am inclined to ignore the findings of the article in the FAJ as valid in theory but implausible in real life. Which brings me to a point of frustration I have had with academics for years. Whether it is Eugene Fama trying to convince the world that the efficient market hypothesis is correct or the authors of the FAJ article trying to convince the world that mean-variance optimization is the best approach to asset allocation: why are academics so adamant that their theories are useful tools for practitioners? Modern portfolio theory with its pillars of the efficient market hypothesis, the CAPM and mean-variance optimization is a great theory and should continue to guide our intuition about how investments ought to work. As such, these theories deserve their place in the list of most important achievements of modern finance. But these theories are built on simplified assumptions about reality that are not met in practice. The real world is messy, and investors need to take the world as it is, not as it should be. Thus, investors need to make adjustments to these theories in order to be successful. No amount of academic arguments or academic fine tuning of existing theories will convince a practitioner to change her approach to investing. Thus, while articles like the one in the FAJ may be useful for a robust debate about the merits of mean-variance optimization, they are, in my view, a waste of time for real life investors.

PS: Please don’t think that I don’t like the FAJ just because I criticise this article. The editor of the FAJ Heidi Raubenheimer and me recently joked that we were probably the only people in the world who read every issue of the FAJ from front to back. This is a shame because I think everyone should read every issue of the FAJ even if there are some articles in there that make your blood pressure rise. This is what research is about: dealing with opinions that you passionately disagree with on a basis of facts and arguments.

Relative error of equity return forecasts

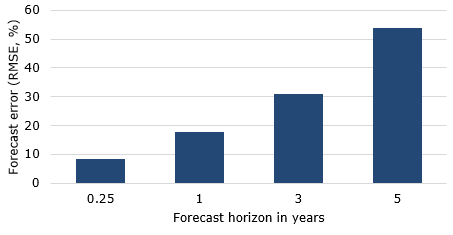
Source: Welch and Goyal (2008).