Yesterday, I talked about how thinking about markets in analogy to thermodynamics leads us to the conclusion that if we take the Second Law of Thermodynamics seriously, share prices should almost never be at or near fair value. Similarly, a market index like the S&P 500 should almost never trade at fair value because it is incredibly unlikely that the valuation of each stock in the market is aligned in such a way that individual mispricings cancel each other out.
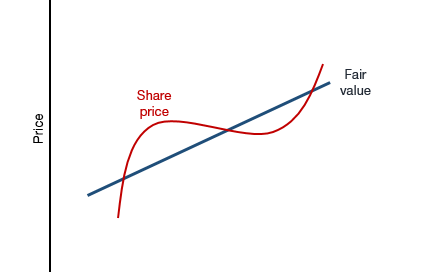
This observation alone does not mean that fair value calculations are useless. If the fluctuations around fair value are more or less random and cancel each other out over time, then calculating the fair value of a stock or a market index is still helpful, because if current prices are too high, one can assume that prices will go down towards fair value over time. This notion is at the heart of the chart below which is one of the most common charts in all of finance. It says that as companies create value for their shareholders over time, the fair value of the company increases and share prices fluctuate around that fair value as investors become too optimistic or too pessimistic for future growth prospects.
The classic way of thinking about markets
Source: Liberum
To make our lives simpler, let’s assume the fair value of the company or the stock market is constant, so we don’t have to deal with that long-term trend and can focus on the variations around that trend. Then we can simply say a fair value model is useful for investors if the deviations of the share price from that fair value over time average out to zero. It might take a long time, but if we wait long enough, the true average of the share prices over time equals the theoretical fair value.
This assumption goes back all the way to the very beginning of finance and economics and Daniel Bernoulli’s description of expected utility theory in 1738. And it links finance to thermodynamics once again because the random deviations from fair value are typically assumed to be drawn from a normal distribution with a given volatility and a given mean. Essentially, the random fluctuations around fair value are modelled mathematically the same way as physicists model the random movements of molecules in a gas or the ink in a water jar that I mentioned yesterday. In technical terms, the random fluctuations around fair value are modelled as Brownian motion.
To understand how these fluctuations are expected to cancel each other out over time, let’s look at a simple coin toss model of a share. Let’s assume the fair value of a company’s share is $100. Because future cash flows of the company are uncertain the share price of the company fluctuates randomly around this fair value. If good news arrives, the share price will increase by 50%, if bad news arrives, it will decrease by 50%. If we look at the expected return of an investment in that share, we expect it to be 0% because while on any given day, the share price may go up 50% or down 50%. Hence, in the long run, the fair value of the share should be the same as the current price of $100. Yes, share prices may go up or down based on the news, but if we wait long enough these deviations from the fair value should cancel each other out and the share price should end up at $100 again.
Easy enough, except that share prices don’t work that way. The average expected return of this investment is indeed 0%, but the average expected wealth of the investor declines the longer the investor holds the stock and eventually approaches zero. This is so because ending wealth is multiplicative, not additive.
Assume you start with one share worth $100. Then some good news arrives and the share price increases by 50% to $150. The next day bad news arrives and the share price drops by 50% to $75. Your average return over the two days was 0%, but your ending wealth after two days is 25% lower than what you started with. Now hold on to your share for longer and you are essentially repeating this over and over again. Your ending wealth will gradually decline and eventually approach zero. And more importantly, the share price will never even remotely approach the theoretical fair value of $100.
Simplified stock value: Fair value vs. ending wealth for investor
Source: Liberum
This is the fundamental error behind the assumption that fair value models are useful as a predictor of the equilibrium price for a stock or the market overall. And it is nowadays increasingly debated under the wonderful term ‘ergodicity problem’. For a deeper treatment of this problem, I highly recommend this article by the guru of ergodicity economics, Ole Peters. Standaed economics and finance theory (aka ‘expected utility economics’) assumes that the expected value of a financial or economic variable is the same as the long-term statistical average of individual observations. ‘Ergodicity economics’ is concerned with instances where this assumption is violated. And as I just showed, this assumption is violated in the most basic approaches to investing.
Does this mean that fair value models are wrong? If ergodicity economics is right, then fair value models are indeed useless and misleading. But if ergodicity economics is right, we would have to revise most of economics and finance developed over the last 250 years. And well-established investment approaches like value investing would turn out to be a historical aberration that worked for 70 years or so but did so more or less by coincidence. If ergodicity theory is correct, the only modern investment approach that – as far as I can see – would survive the onslaught is momentum investing and trend following because that essentially makes no assumption about the fair value of an asset at all.
But I am not ready to throw fair value models out the window just yet. Ergodicity economics is a very young discipline and lots of work still lies ahead of us. Furthermore, expected utility economics and related concepts like fair value models have served investors well for a long time. It takes an enormous amount of empirical evidence that expected utility theory is violated in real life before we abandon it. And we are not there, yet, but as I will show tomorrow, there is one experiment that showed how expected utility economics is violated. So, we may at least be doubtful about fair value models and their practical relevance and maybe adjust our investment processes accordingly.





I've always felt that concepts such as calculating 'fair value' are as useful as beating myself in the face with a dead fish (but less amusing and at the end of all the calculations I still don't have a fish). This article explains why in proper grown-up words rather than my exasperated tut-tuting and eye rolling.
...ok so should I use a haddock or a trout today?......
Am I naive or is the ending wealth problem based on a card trick? If we switch from 50% up and 50% down to $50 up and $50 down, the problem goes away, doesn't it? And doesn't the $ approach make more sense than the % approach?